I. Introdução
Água pode acender velas, é verdade? É verdade!
É verdade que as cobras têm medo de realgar? Isso é falso!
O que vamos discutir hoje é:
É verdade que a interferência pode melhorar a precisão das medições?
Em circunstâncias normais, a interferência é o inimigo natural da medição. A interferência reduz a precisão da medição. Em casos graves, a medição não será realizada normalmente. Desse ponto de vista, afirmar que a interferência pode melhorar a precisão da medição é um equívoco!
No entanto, será que isso é sempre verdade? Existe alguma situação em que a interferência não reduza a precisão da medição, mas, ao contrário, a melhore?
Sim, a resposta é!
2. Acordo de Interferência
Considerando a situação atual, chegamos ao seguinte acordo sobre a interferência:
- A interferência não contém componentes CC. Na medição real, a interferência é principalmente CA, e essa suposição é razoável.
- Comparada com a tensão CC medida, a amplitude da interferência é relativamente pequena. Isso está de acordo com a situação real.
- A interferência é um sinal periódico, ou seja, seu valor médio é zero dentro de um período de tempo fixo. Isso não é necessariamente verdade em medições reais. No entanto, como a interferência geralmente é um sinal CA de frequência mais alta, para a maioria das interferências, a convenção de média zero é razoável por um período de tempo mais longo.
3. Precisão de medição sob interferência
A maioria dos instrumentos e medidores elétricos atuais utiliza conversores AD, e sua precisão de medição está intimamente relacionada à resolução do conversor AD. De modo geral, conversores AD com maior resolução apresentam maior precisão de medição.
No entanto, a resolução de um conversor AD é sempre limitada. Supondo que a resolução de um conversor AD seja de 3 bits e a tensão máxima de medição seja de 8V, o conversor AD é equivalente a uma escala dividida em 8 partes, cada uma com incrementos de 1V. O resultado da medição deste conversor AD é sempre um número inteiro, e a parte decimal é sempre transportada ou descartada (neste trabalho, consideramos que será transportada). O transporte ou descarte da parte decimal causará erros de medição. Por exemplo, se 6,3V for maior que 6V e menor que 7V, o resultado da medição do conversor AD será 7V, resultando em um erro de 0,7V. Chamamos esse erro de erro de quantização do conversor AD.
Para facilitar a análise, assumimos que a balança (conversor AD) não apresenta outros erros de medição além do erro de quantização do conversor AD.
Agora, utilizamos duas escalas idênticas para medir as duas tensões CC mostradas na Figura 1 sem interferência (situação ideal) e com interferência.
Como mostrado na Figura 1, a tensão CC medida é de 6,3 V, e a tensão CC na figura à esquerda não apresenta interferências, mantendo-se constante. A figura à direita mostra a corrente contínua perturbada pela corrente alternada, apresentando uma certa flutuação no valor. A tensão CC no diagrama à direita é igual à tensão CC no diagrama à esquerda após a eliminação do sinal de interferência. O quadrado vermelho na figura representa o resultado da conversão do conversor AD.

Tensão CC ideal sem interferências
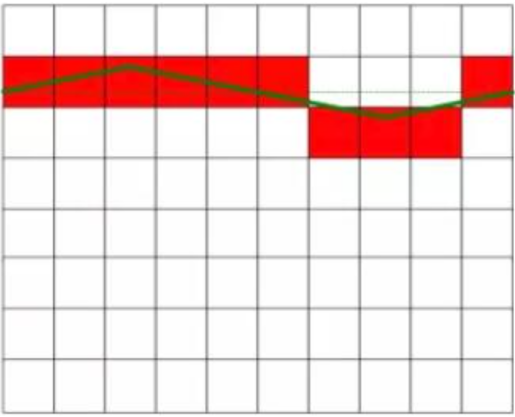
Aplique uma tensão CC interferente com valor médio zero.
Faça 10 medições da corrente contínua nos dois casos da figura acima e, em seguida, calcule a média das 10 medições.
A primeira escala à esquerda foi medida 10 vezes, e as leituras foram sempre as mesmas. Devido à influência do erro de quantização do conversor AD, cada leitura foi de 7V. Após a média das 10 medições, o resultado continuou sendo 7V. O erro de quantização do conversor AD foi de 0,7V, e o erro de medição também foi de 0,7V.
A segunda escala à direita mudou drasticamente:
Devido à diferença entre os valores positivos e negativos da tensão de interferência e da amplitude, o erro de quantização do conversor analógico-digital (AD) varia em diferentes pontos de medição. Com a variação do erro de quantização do AD, o resultado da medição oscila entre 6V e 7V. Sete das medições apresentaram 7V, apenas três apresentaram 6V, e a média das 10 medições foi de 6,3V! O erro é de 0V!
Na verdade, nenhum erro é impossível, porque no mundo objetivo não existe um valor estrito de 6,3V! No entanto, existem, sim:
Na ausência de interferências, visto que cada resultado de medição é o mesmo, após calcular a média de 10 medições, o erro permanece inalterado!
Quando há uma quantidade adequada de interferência, após a média de 10 medições, o erro de quantização do conversor analógico-digital é reduzido em uma ordem de magnitude! A resolução é melhorada em uma ordem de magnitude! A precisão da medição também é melhorada em uma ordem de magnitude!
As principais questões são:
O mesmo ocorre quando a tensão medida apresenta outros valores?
Os leitores podem optar por seguir o acordo sobre interferência na segunda seção, expressando a interferência com uma série de valores numéricos, sobrepondo a interferência à tensão medida e, em seguida, calculando os resultados da medição de cada ponto de acordo com o princípio de transporte do conversor AD. Depois, devem calcular o valor médio para verificação. Contanto que a amplitude da interferência possa causar uma alteração na leitura após a quantização do conversor AD e a frequência de amostragem seja suficientemente alta (as alterações na amplitude da interferência apresentem um processo de transição, em vez de dois valores, positivo e negativo), a precisão certamente será melhorada!
Pode-se provar que, enquanto a tensão medida não for exatamente um número inteiro (pois não existe no mundo objetivo), haverá erro de quantização do conversor analógico-digital (AD). Independentemente da magnitude desse erro, desde que a amplitude da interferência seja maior que o erro de quantização do AD ou maior que a resolução mínima do conversor AD, o resultado da medição oscilará entre dois valores adjacentes. Como a interferência é simétrica em relação à polaridade (positiva e negativa), a magnitude e a probabilidade de diminuição e aumento são iguais. Portanto, quanto mais próximo o valor real estiver de um determinado valor, maior será a probabilidade de o valor real aparecer, e, após a média, o valor real estará próximo desse valor.
Ou seja: o valor médio de múltiplas medições (valor médio da interferência igual a zero) deve estar mais próximo do resultado da medição sem interferência. Em outras palavras, usar o sinal de interferência CA com valor médio zero e calcular a média de múltiplas medições pode reduzir os erros de quantização equivalentes do conversor analógico-digital (AD), melhorar a resolução da medição do AD e aumentar a precisão da medição!
Data da publicação: 13 de julho de 2023




